Did you solve it? Oxford university admissions questions

Earlier today I set the following three puzzles, which have all been set during Oxford university admissions interviews for joint philosophy courses. In each case, there is an initial question, which almost all candidates answer correctly. The follow-up questions are more challenging.

1. Stephanie’s surprise.

Stephanie has invited her friends Rowan and Colleen to her home. They are all perfectly logical. She tells them that she has hidden a surprise under one of the blue squares.

Stephanie has privately told Rowan the row number of the surprise and Colleen the column letter of the surprise, and everyone is aware of this. The following conversation ensues.

Rowan: I don’t know where the surprise is, but I also know that Colleen doesn’t know.

Colleen: Yes, indeed, at first I didn’t know the location of the surprise. But now I know where it is.

Rowan: In that case, I now also know where it must be.

Question. Where is the surprise?

Follow up: Suppose that before any conversation took place, someone trips over B1, which opens, revealing it to be empty. a) Could the conversation have proceeded as before? b) Were either of them surprised to see it empty? c) How can it have changed the conversation, if they both knew it already. d) How can it be that adding information, that B1 is empty, makes Rowan’s statement become false? (This is the most interesting aspect of the puzzle, since it seems paradoxical that adding information can reduce knowledge.)

Solution Under square A2

If Rowan doesn’t know where the surprise is we can eliminate row 3 (since if he was told row 3 he would know the correct square.) If he knows that Colleen doesnt know, we can eliminate row 4 (since only way it would be possible for Collen to know the correct square at the start is if it was C4.) If Colleen now knows the correct square, she must know the column for which there is only one option left. This column is A, and thus the correct square is A2.

Follow up: a) No. The second part of Rowan’s first statement is now false. b) No. They both knew that B1 wasn’t the tile. c) Because they are learning knowledge about knowledge. d) The knowledge that Rowan had was that Colleen didn’t know something – and the extra information gleaned meant that he lost that knowledge, because it meant he didn’t know she didn’t know. The extra information might have given her knowledge, for example, if it had been B2, she would have known after seeing B1 empty.

2. Tile party.

At a party for our perfectly logical philosophy friends Sheila and Colin, a surprise has been hidden under one of these coloured tiles:

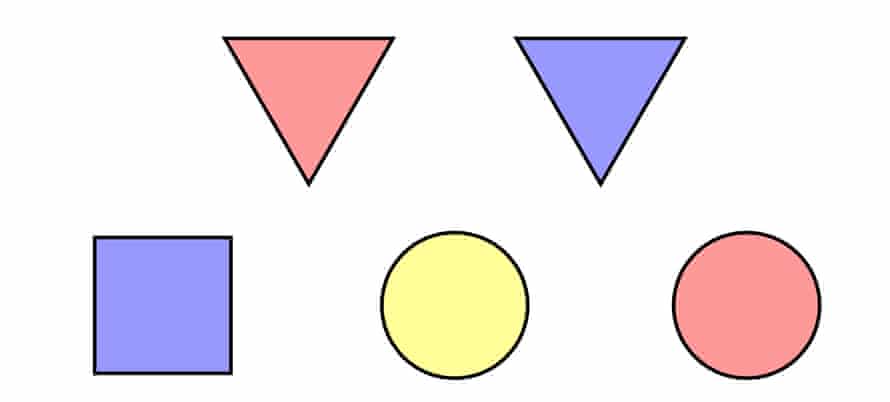
Each friend is privately told a piece of information about where the surprise is. ????

It is commonly known by all that this and no other information is given.

Host: Do either of you know where the surprise is?

. . . Awkward long silence. . .

Host: Do you know now?

. . . More awkward silence. . .

Sheila, Colin: (simultaneously): Now I know where it is!

Question. Where is the surprise?

Follow up: a) Did either of them expect the first silence? b) What effect on their knowledge did that silence serve? How did they learn anything from it? c) Did Colin know that Sheila knew that Colin didn’t know initially where the surprise was? d) Did either of them expect the second silence?

Solution: The surprise is under the red triangle.

The only way that Sheila could know the correct tile before the dialogue is if she had been told ‘square’, and the only way that Colin could know is if he had been told ‘yellow’. Since they are silent when the host asks the first question we assume that they don’t know the correct tile, and thus we can eliminate the square and the yellow tiles. If Sheila had been told ‘circle’ she would now know the correct tile, because there is only one circle left. If Colin had been told ‘blue’ he would also know the correct tile. However since both of them remain silent when the host asks the second question, we can assume that they don’t know the correct tile, and thus we deduce that the tile must be red and a triangle.

a) Yes. Sheila knows initially that Colin does not know where the surprise is, because both triangular tiles have a partner tile of the same colour. Likewise Colin knows Sheila does not know where the surprise is because she knows it’s red, and both red tiles have a partner tile of same shape. b) What they learned from it was the knowledge that the other person now knew that they hadn’t known the location. c) No, because although he knew it was red, it might have been the red circle, in which case Sheila wouldn’t have known that Colin didn’t know, since she might have thought it could have been the yellow circle. d) No, neither did. From Colin’s perspective, it could have been red circle, in which case Sheila would have answered after the first silence, but she didn’t. From Sheila’s perspective, it could have been the blue triangle, in which case Colin would have answered after the first silence, but he didn’t.

3. Alice’s boxes.

Alice has invited her friends Caroline and Susan to her home, and she has placed several boxes on the table before them. They are all perfectly logical.

• small red box

• medium red box

• large black box

• small blue box

• large blue box

Alice tells her friends that she has placed a gift into one of the boxes, and she has privately told Caroline the colour of the box and Susan the size of the box, and they both know this. The following conversation ensues.

Caroline: I don’t know which box contains the gift, and I also know that Susan doesn’t know.

Susan: I already knew before you spoke that you didn’t know which box contains the gift.

Caroline: Ah, now that you say that, it suddenly occurs to me which box must contain the gift.

Question. Which box contains the gift?

Follow up: After the conversation, does Susan also know which box contains the gift? If so, who came to the knowledge first, Caroline or Susan?

Solution small blue box

This puzzle appears more difficult because there is no illustration. So to make it easier, draw out a 3×3 grid in which red, black and blue are the columns and small, medium and large the rows. The possible boxes, marked X, are thus

If Caroline doesnt know the box, she cannot have been told ‘black’. And if she knows Susan doesn’t know, Caroline can’t have been told ‘red’, since if she had been told ‘red’ then then there is a chance Susan had been told ‘medium’, in which case Caroline would not be able to say that she knows Susan doesn’t know. So we deduce Caroline was told ‘blue’.

Now if, before Caroline spoke, Susan knew that Caroline didn’t know the correct box, we can eliminate the possibility that Susan was told ‘large’. Since if she had been told ‘large’ she would not know for certain that Caroline didn’t know, since she cannot rule out the possibility that the large black box has the gift, in which case Caroline would know. Since the box is blue and not large, the only remaining option is small and blue.

Susan knows the correct box first. She knows it as soon as Caroline has spoken her first sentence, since after that statement Susan knows the box is blue. And since she knows the box is small, it can only be the small blue box.

Thanks again to the author of these puzzles, Joel David Hamkins, who is Oxford’s Professor of Logic and the Sir Peter Strawson Fellow in Philosophy at University College, Oxford. You can find more about his work on his personal website.

I set a puzzle here every two weeks on a Monday. I’m always on the look-out for great puzzles. If you would like to suggest one, email me.

I’m the author of several books of puzzles, most recently the Language Lover’s Puzzle Book. I also give school talks about maths and puzzles (restrictions allowing). If your school is interested please get in touch.